Правило Байеса и водопады: легкий способ начать мыслить вероятностями и шансами

Идею с водопадами мы с благодарностью взяли отсюда: arbital.com/p/bayes_rule/?l=1zq

В статье про оптимизацию ценообразования мы решали такую задачу:

Допустим, вы сдаете тест на наличие антител к коронавирусу.
Пусть 1% людей, сдающих тесты на антитела к коронавирусу, обладают такими антителами (специальный показатель у них превышает пороговое значение).
90% людей с антителами получают положительный результат: антитела есть.
9% людей без антител также получают положительный результат теста: тест говорит "антитела есть", хотя их нет.

Вы сдали тест и получили положительный результат: антитела есть.
Какова вероятность того, что у вас действительно есть антитела?

Ниже - обещанный лёгкий способ решения.
Пройдя его один раз, вы навсегда (ну, надолго) перестанете путаться в долях и вероятностях.

Представьте водопад, вверху которого две речки, красная и синяя.

Реки приходят к вершине водопада по отдельности.

Часть воды из обеих рек уходит в стороны.

Оставшаяся вода падает в общий бассейн в центре, превращаясь в фиолетовую.

Задача:

Пусть из рек в водопад каждую секунду стекает 99 литров синей воды и 1 литр красной воды.

Часть воды уходит в стороны из-за камней; на дно в центр водопада приходит только 9% синей воды и 90% красной воды.

Какая доля фиолетовой воды на дне, намешавшейся из воды двух цветов, приходит из красной реки и какая доля из синей?

Путь решения очевиден:

1. В бассейн в центре приходит 8,91 литра синей воды
(99 литров * 9% = 8,91 литра)

2. Красной воды туда поступает 0,9 литра
(1 литр * 90% = 0,9 литра)

Теперь считаем пропорцию:

Каждую секунду в центре прибавляется 9,81 литров фиолетовой воды
(8,91 + 0,9 = 9,81 литр фиолетовой воды, смешавшейся из красной и синей)

~91% - доля синей воды в фиолетовой
(8,91 / 9,81 ≈ 0,91 )

~9% - доля красной воды в фиолетовой
(0,9 / 9,81 ≈ 0,09)

Итого доли в фиолетовой воде соотносятся:
91 синей : 9 красной

Задачу про антитела легко преобразовать в задачу о водопадах:

на вершину водопада ставим исходные доли людей, сдающих тест на антитела:
1% с антителами и 99% без антител
(100% - 1% = 99%)

Вы получили положительный тест на антитела.
Вероятность, что они у вас действительно есть, ≈9%
это доля "красной воды" в "фиолетовой воде":

Иногда можно решить ещё проще:

В решении важны только пропорции чисел, а не сами числа.

Исходные пропорции:
99 : 1 - здесь нечего сокращать, оба числа - простые.
9 : 90 - здесь оба числа кратны девятке, можно её сократить.

Получаем:
99 : 1 - исходная пропорция обеих рек
1 : 10 - пропорция "кусочков" рек, попадающих в бассейн в центре.

Умножаем (99 : 1 ) * (1 : 10) = (99 * 1) : (1 * 10) = 99 : 10

Фиолетовый бассейн состоит из 99 частей синей воды и из 10 частей красной воды. Переведем полученную пропорцию 99 : 10 в вероятность, что случайная молекула на дне окажется красной:

10/ (10+99) = 10/109

Итак, 10/109 (около 9%) воды приходит в фиолетовый бассейн из красной речки.

10/109 ≈ 9% - вероятность, что у вас действительно есть антитела, если ваш тест на антитела - положительный.

Для закрепления навыка попробуйте проделать аналогичные вычисления в уме для других условий:

У 10% людей, сдающих тесты на антитела к коронавирусу, есть антитела, а у 90% - нет.
90% людей с антителами получают положительный результат: антитела есть.
9% людей без антител также получают положительный результат теста: тест говорит "антитела есть", хотя их нет.

Вы в числе тестировавшихся и получили положительный тест.
Какова вероятность, что у вас действительно есть антитела?

(Должно получиться 10/19,
что приблизительно равно 52,6%)

Правило Байеса и формула Байеса

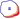
Водопады - это просто способ визуализации «в виде шансов» «правила Байеса»:

Апостериорные шансы = Априорные шансы * Относительные частоты

| - знак условия. Например, P(A | E) - это вероятность наступления события А при условии, что уже наступило событие Е.

Отсюда

Избавимся от членов с событием В.
С помощью формулы условной вероятности:

заменяем P(B | E) и P(E | B) на соответствующие дроби.
После сокращений одинаковых величин получаем Формулу Байеса, показывающую, как нужно изменить вероятность события А, если мы знаем, что наступило событие Е:

Вероятность наступления события A при условии, что наступило событие Е, равна вероятности наступления события A, умноженной на вероятность наступления события Е при условии, что наступило событие A, и деленной на вероятность наступления Е.

Повторим важный тезис:

Правило Байеса указывает, насколько следует пересмотреть интересующие нас вероятности какого-то события (изменить свою оценку ситуации), когда мы узнаём новый факт или получаем новые данные.

Вернуться в статью об Оптимизации ценообразования